Neural Field Convolutions by Repeated Differentiation

ACM Transactions on Graphics (Proceedings of SIGGRAPH Asia), 2023

Ntumba Elie Nsampi1, Adarsh Djeacoumar1, Hans-Peter Seidel1, Tobias Ritschel2, Thomas Leimkühler1
1Max-Planck-Institut für Informatik, 2University College London
Paper Code

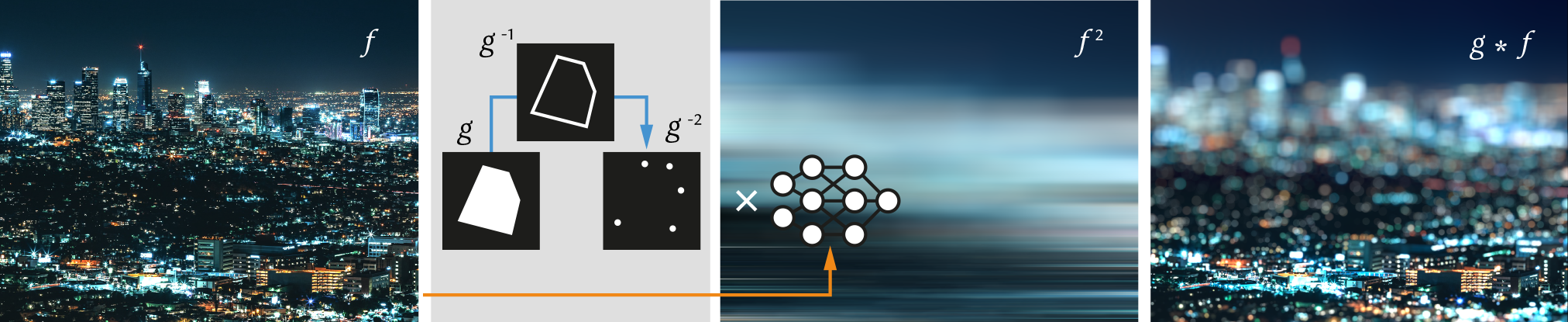
We introduce an algorithm to perform efficient continuous convolution of neural fields 𝑓 by piecewise polynomial kernels 𝑔. The key idea is to convolve the sparse repeated derivative of the kernel with the repeated antiderivative of the signal.

Abstract

Neural fields are evolving towards a general-purpose continuous representation for visual computing. Yet, despite their numerous appealing properties, they are hardly amenable to signal processing. As a remedy, we present a method to perform general continuous convolutions with general continuous signals such as neural fields. Observing that piecewise polynomial kernels reduce to a sparse set of Dirac deltas after repeated differentiation, we leverage convolution identities and train a repeated integral field to efficiently execute large-scale convolutions. We demonstrate our approach on a variety of data modalities and spatially-varying kernels.

Method

a) Given an arbitrary convolution kernel, we optimize for its piecewise polynomial approximation, which under repeated differentiation yields a sparse set of Dirac deltas. b) Given an original signal, we train a neural field which captures the repeated integral of the signal. c) The continuous convolution of the original signal and the convolution kernel is obtained by a discrete convolution of the sparse Dirac deltas from a) and corresponding sparse samples of the neural integral field from b).

Applications

Images

Images can be represented using Neural Fields that map 2D location to RGB color. Below we perform a Scale-space sweep, i.e. Continuous control over kernel size.


Geometry

We represent surfaces using Neural Signed Distance Fields (NSDFs) Which we filter using 3D box filters. Below we perform a Scale-space sweep, i.e. Continuous control over kernel size.

Videos

We represent videos using Neural Fields mapping 2D location and time to RGB color. By applying a smoothing filter along the time dimension, we are able to create appealing non-linear motion blur.

σ = 0.2

σ = 0.5

Animation

We consider the task of filtering a Neural Field representation of a noisy motion-capture sequence which consists of 23 3D joint position paths over time resulting in a field mapping time to joint position. We obtain smooth motion trajectories by applying a Gaussian Filter to the Neural representation.

Left: Original noisy motion capture data. Right: Our filtered result.

Audio

Audio Signal can be represented using Neural Fields mapping time to sound intensity. Below we apply our framework to an audio signal.

Left: Original. Center: Low-pass reference. Right: Our low-pass filtered result.


Errata

It has unfortunately come to our attention that our results as reported in Table 3 and Fig. 16. contained some errors. We have since corrected these errors in both our arXiv manuscipt and in the manuscript provided on this webpage. Please be aware that while these two manuscripts reflect the corrections, the published version of our work still contains the aforementioned errors.


BibTeX


    @article{Nsampi2023NeuralFC,
      author = {Ntumba Elie Nsampi and Adarsh Djeacoumar and Hans-Peter Seidel and Tobias Ritschel and Thomas Leimk{\"u}hler},
      title = {Neural Field Convolutions by Repeated Differentiation},
      year = {2023},
      issue_date = {December 2023},
      publisher = {Association for Computing Machinery},
      address = {Sydney, Australia},
      volume = {42},
      number = {6},
      issn = {},
      url = {https://doi.org/10.1145/3618340},
      doi = {10.1145/3618340},
      journal = {ACM Trans. Graph.},
      month = {Dec},
      articleno = {206},
      numpages = {11},
}